PROBLEMA 32
Notación y terminología:
E(x) : Función Generatriz
Exponencial
: Sucesión asociada a
la función
Antecedentes: debemos considerar las expresiones
generales de Funciones Generatrices Exponenciales y series de Maclaurin para 
y 
PREGUNTA 32.
Demuestre que la Función
Generatriz Exponencial para 
, 
= numero de i-palabras de { a,b,c,d } con un número par de d’s y un número impar
de c’s es 
RESPUESTA 32.
La suma de las i-permutaciones de { a,b,c,d } es:
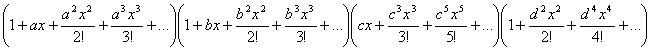
si a=b=c=d=1 en la expansión quedaría:
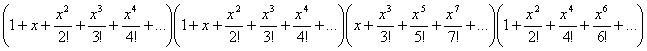
Considerando los
desarrollos en serie de Maclaurin:
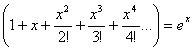y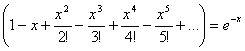 
si sumamos estas series, obtenemos
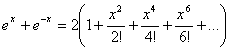o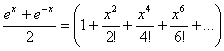 
si restamos 
de , tenemos que
Entonces la suma de las i-permutaciones
nos quedaría
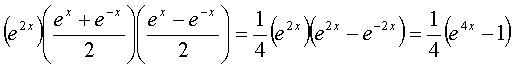
Moraleja: Para poder resolver este tipo de problemas hay que madurar
bien el concepto de funciones generatrices y tener presente los conocimientos
sobre Series del curso de calculo40.